Probability of Dice Rolls in Settlers of Catan

A few weeks back I played a game of Settler of Catan where an 8 was only rolled once. This is a pretty big deal if you know how the game is played.
In Settlers of Catan, each turn begins with a player rolling two 6-sided dice. The sum of this roll determines the game play. The full rules of the game aren’t important for this post, just the fact that players hedge their play based on the probabilities of specific sums occurring. According to these probabilities an 8 should roll, on average, every 7.2 turns. In our game it took 72 turns to roll an 8! For the players who had hedged their fortunes on 8s, this was a crushing blow.
After the game we spent some time discussing the rarity of a game such as this. Many felt that only rolling one 8 in 72 turns was incredibly rare. I argued that it wasn’t as rare as we might think. I then took the position that we couldn’t have a logical discussion about these kind of games since randomness was involved. I was wrong, we have probability theory.
Let’s explore probability theory to learn how rare this game really was.
Single Die Probabilities
When rolling a single 6-sided die, the chance of rolling any side is equal. Since there are six sides to the die, each side has a 1 out of 6 chance of rolling. If, say, we were to roll a single die 600 times, each side would appear on average 100 times.
In probability theory terms this is called a uniform distribution.
Dice Sum Probabilities
Things get more interesting when pairs of dice are thrown and summed, as in Settlers. In this situation certain sums are more likely to appear than others. This is because there are more possible die-side combinations for certain sums.
The following chart shows this distribution of sums. Notice that the sum of two uniform distributions (each die) makes a triangular distribution.
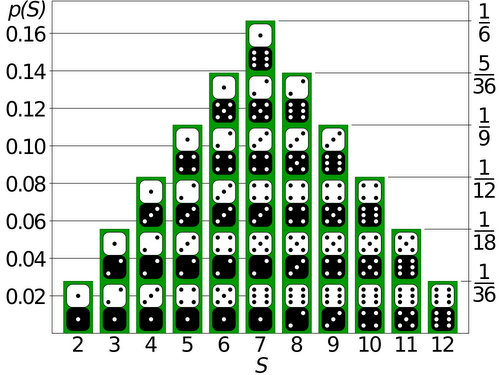
Shown in this image are the 36 possible outcomes of rolling 2 dice. Six of these combos sum to a 7 while only one of them sums to a 2. It should therefore be apparent that in a game of Settlers, 7s are rolled more often than 2s. If you don’t believe me, grab a pair of dice and start rolling while keeping track of the sums.
Looking at this chart we see that 5 of the 36 possible combinations sum to an 8. As such, an 8 should roll on average 5 times every 36 rolls, or as I stated earlier, once every 7.2 rolls (5/36).
Simulating Dice Rolls
I coded the following visualization to demonstrates these dice-sum probabilities. In this program virtual 6-sided dice-throws are simulated using a pseudorandom number generator. In total over 3000 virtual dice are thrown before the programs resets.
The left-hand graph above shows how often each virtual die lands on a specific side, 1 through 6. Since there is an equal probability of each side appearing, the columns in this graph should all be approximately the same height. This is the uniform distribution I mentioned earlier.
The right-hand graph above shows these same dice-rolls grouped in pairs and summed, just like in a game of Settlers. As the number of rolls increases, this graph of sum-occurrences begins to resemble the triangular distribution shown in picture of the dice sum combos above.
Randomness is Tricky
Based on these dice-sum probabilities, how often should an 8 roll in 72 turns? Well, if the chance of rolling an 8 is 5 out of 36 (or 13.9%) then in 72 turns an eight should roll on average 10 times. Why? Because 13.9% of 72 is 10.
Notice that throughout this post I’ve been using the phrase “on average” when talking about expected dice rolls? That’s the key to our mystery. Yes, based on the probabilities, an 8 should be rolled 13.9% of the time. However, each roll is random and independent from all previous rolls. So with enough rolls these probabilities will be true, but for a small sampling of rolls they may not be. Grab two dice and roll them 36 times, a sum of 8 won’t always show up exactly 5 times. Such is chaos.
The next visualization demonstrates just this effect. Each refresh of the graphs represents another possible 72-roll game of Settlers. With a sample size of 72 pairs of dice the graphs are often far from ideal. In some games dice-sides are far from uniform, and the dice sums do not always follow the expected triangular probability distribution.
Our Crazy Game
So how rare was our game? I used the AnyDice programming language (which is an amazing tool btw) to find out.
output 72d (2d6 = 8)
This program calculates the odds of rolling any number of 8s in a game of 72 rolls of 2 six-sided dice. Based on the output of this program the odds of rolling only one 8 in a 72 turn game of Settlers is 0.0245020661348%. In other words, a game like this could be expected once every 4,081 games.
Truthfully, since our game went to 79 rolls it was more like a 1 out of 10,594 game. Had no eights rolled in the entire 79 roll game, it would have been a 1 out of 135,000 game. Rare, but still possible. Such is chaos.
UPDATE (18/12/2013): What About The Sequence of No-8 Rolls?
After reading this post, a friend who was at the game suggested that the odds were actually far worse than I calculated, if you take the order of the rolls into account. His argument being that a run of 71 no-8 rolls is a 1 in 40,813 event. See calculation below*.
While this is true, it’s important to note that we are now talking about two different probabilities.
- Probability of a sequence of 71 no-8 rolls: 1 in 40,813
- Probability of rolling only one 8 anywhere in 79 rolls: 1 in 10,594
Resources and Further Reading
Before I started writing this blog post I wrote a Ruby program to simulate the roll of dice in Settlers using the truly random data from Random.org.
I referenced the following sites while writing this post:
- Understanding Probability
- Dice Odds for Settlers of Catan
- These dice are driving me crazy!
- Central Limit Theorem
- Two Dice Roll Calculator
- Triangle Distribution - The Sum of Random Variables
*Example Probability Calculation: The odds of rolling no 8s in a game of 71 turns.
The probability of not rolling an 8 is 1 minus the probability of rolling an 8.
1 - 5/36 = 31/36
We multiply the probability of not rolling an 8 with itself 71 times (31/36 to the power of 71) to find our answer.
The odds are 0.00245020661348% which is 1 out of 40,813.
Attributions: The header image for this post was found on enjoyneer.blogspot.ca. The dice-sum probability image was found on rosalind.info. I wrote the two programs in this post using the Processing language and they are hosted on OpenProcessing.org.
Over the years my dad has found a number of older intaglio copperplates in various Dutch markets. Once back home, he cleans them up and prints them at his studio in the Artspace building.
This is a print of his latest find, a copperplate etching printed on rag paper.
Related: Etching for Artists and Hackers - The slides from a 2011 presentation I gave at Skullspace.

